击败 LLM 推理中的非确定性：从“玄学”到可控

在科学研究和工程实践中，可复现性（Reproducibility）无疑是衡量结果可靠性的黄金标准。然而，当我们步入大语言模型（LLM）的奇妙世界时，这个看似理所当然的基石却摇摇欲坠。你有没有发现，即便是向同一个 LLM 反复提出同一个问题，得到的答案也常常是“变幻莫测”的？这不禁让人疑惑：难道 LLM 的输出注定是一场“玄学”吗？

初次接触时，我们或许会归咎于 LLM 推理中的“采样”机制——它将模型的输出转化为概率分布，然后随机挑选一个 token。这听起来合情合理，毕竟概率事件本就带有随机性。但更令人费解的是，即使我们将采样温度（temperature）严格设置为 0（理论上，这意味着模型会“贪婪”地选择概率最高的 token，从而实现确定性输出），LLM API 的实际表现依然非确定。无论是在像 ChatGPT 这样的在线服务中，还是使用 vLLM、SGLang 等开源推理库在本地硬件上运行，我们都无法完全摆脱这种非确定性困扰。

那么，究竟是什么原因让 LLM 推理如此“不靠谱”？一个流传甚广的假设是，浮点数的非结合性（non-associativity）与并发执行（concurrent execution）的“合谋”。这个“并发 + 浮点数”假说认为，在 GPU 上并行计算时，由于浮点数的有限精度和舍入误差，不同并发核心完成计算的顺序不同，会导致累加顺序变化，进而产生最终结果的差异。比如，最近一篇预印本就提到：

GPU 中的浮点算术表现出非结合性，这意味着 $(a + b) + c \neq a + (b + c)$。由于有限精度和舍入误差，这个特性直接影响 Transformer 架构中注意力分数和 logits 的计算，其中多个线程的并行操作可能会根据执行顺序产生不同的结果。

这种观点并非空穴来风，很多技术讨论也都支持类似看法。然而，仅仅归咎于“并发 + 浮点数”并不能完全揭示真相。举个简单的例子，如果我们在 GPU 上对相同的矩阵重复执行多次矩阵乘法，结果始终是位级别（bitwise）相同的。这让人疑惑：明明同样涉及浮点数和大并发，为何这里就没有非确定性呢？

A = torch.randn(2048, 2048, device='cuda', dtype=torch.bfloat16)
B = torch.randn(2048, 2048, device='cuda', dtype=torch.bfloat16)
ref = torch.mm(A, B)
for _ in range(1000):
    assert (torch.mm(A, B) - ref).abs().max().item() == 0

要真正理解 LLM 推理非确定性的根源，我们需要更深层次的探索。有趣的是，即使是定义 LLM 推理的确定性本身就充满挑战。以下这些看似矛盾的陈述，却都同时成立：

1. GPU 上的一些计算核心（kernel）确实可能非确定。

2. 然而，LLM 前向传播中使用的所有核心（kernel）实际上是确定性的。

3. 更进一步，LLM 推理服务器（如 vLLM）的整个前向传播过程也可以被认为是确定性的。

4. 但从用户的角度看，推理结果却依然非确定。

这篇深入文章将逐步剖析“并发 + 浮点数”假说为何未能触及本质，揭露 LLM 推理非确定性的真正幕后黑手，并最终指导我们如何“击败”这种非确定性，从而在 LLM 推理中获得真正可复现、可控的结果。

1. 浮点数：确定性计算的“原始之罪”

在深究非确定性之前，我们有必要先弄清楚数值差异为何会产生。我们习惯于将机器学习模型视为遵循严格数学规则（如交换律、结合律）的函数。那么，我们的机器学习库难道不应该给出“数学上正确”的结果吗？

问题的核心在于浮点数的非结合性。简单来说，在浮点数运算中，$(a + b) + c$ 可能不等于 $a + (b + c)$。这在直观上可能难以接受，但却是浮点数运算的固有特性。

(0.1 + 1e20) - 1e20
>>> 0
0.1 + (1e20 - 1e20)
>>> 0.1

讽刺的是，正是这种“打破结合律”的特性，才让浮点数在实际应用中显得如此强大。浮点数通过“动态精度”来表示数值，即在有限的存储空间内，能够同时表示非常大和非常小的数字。以十进制为例（为便于理解，这里假设尾数 3 位，指数 1 位），像 3450 可以表示为 $3.45 imes 10^3$，而 0.486 则表示为 $4.86 imes 10^{-1}$。这种表示方式使得我们能在大范围数值中保持近似恒定的“有效数字”数量。

然而，当我们将不同数量级的浮点数相加时，问题就出现了。例如，1230 和 23.4 的精确和是 1253.4。但在只有 3 位精度的浮点数系统中，我们可能只能表示为 $1.25 imes 10^3$（即 1250），末尾的 34 被丢弃了。这相当于在相加前，23.4 被“四舍五入”成了 20.0。这种信息损失每次发生在不同数量级的浮点数相加时，都会导致精度问题。试想，如果每次运算都能保证数量级相同，我们直接用整数不就好了吗？

这意味着，每次我们以不同的顺序进行浮点数累加，都可能产生完全不同的结果。一个极端的例子是，对一个包含正负数的小数组求和，仅仅改变加法顺序，就可能得到上百种不同的结果：

import random

vals = [1e-10, 1e-5, 1e-2, 1]
vals = vals + [-v for v in vals]

results = []
random.seed(42)
for _ in range(10000):
    random.shuffle(vals)
    results.append(sum(vals))

results = sorted(set(results))
print(f"There are {len(results)} unique results: {results}")

虽然浮点数非结合性是导致数值差异的根本原因，但它并没有直接解释 LLM 推理非确定性的来源——即为什么浮点数会以不同的顺序被累加，以及何时会发生，又该如何避免。要回答这些问题，我们需要深入了解 GPU 内核（kernel）的实现方式。

2. 内核（Kernel）执行：原子操作的“陷阱”与并行归约的“救赎”

如前所述，“并发 + 浮点数”假说认为，GPU 的并发执行可能导致浮点数累加顺序的不确定性。然而，实际情况远比这复杂。令人意外的是，并发（以及原子加法）在 LLM 推理的非确定性中，最终扮演的角色却微乎其微！要揭示真正的罪魁祸首，我们首先要理解为什么现代 GPU 内核很少需要依赖原子加法。

通常，GPU 会在大量的“核心”（例如 CUDA 核心或流多处理器）上并行执行计算任务。当需要对一个大型数组进行求和时，一个常见的策略是让每个核心处理数组的一部分，计算出各自的“部分和”，然后再将这些部分和汇总得到最终结果。理论上，这些“部分和”可以通过原子加法（atomic add）进行累加。原子加法虽然能确保数据一致性，但其固有的串行特性导致效率低下，因此，现代 GPU 内核通常采用并行归约（parallel reduction）的方式来累加部分和。并行归约是一种巧妙的算法，它能以固定且可预测的顺序完成累加，从而保证了计算结果的确定性。

然而，这并非绝对。有些内核确实可能表现出真正的非确定性行为。例如，在一个将值映射到计数（如哈希表）的累加操作中，如果多个并发线程同时尝试写入同一个位置，那么最终结果将取决于线程写入的顺序。这类操作会引入真正的非确定性。但值得庆幸的是，在 LLM 推理的算子实现中，这类真正的非确定性内核并未被广泛使用。通常情况下，LLM 推理中的底层计算内核都是确定性的。

3. 为什么确定性内核会产生非确定性结果？

既然我们已经明确，LLM 推理中大多数底层计算内核都是确定性的，那么为何最终的推理结果却依然“非确定”呢？这看起来像是一个悖论。

关键在于我们如何定义“确定性内核”。一个具有“确定性行为”的内核，意味着如果它的输入是位级别（bitwise）相同的，那么其输出也必定是位级别相同的。换言之，它表现得像一个纯函数（pure function）。

然而，问题的症结在于，内核的输入并非总是来自“纯净”的源头。如果内核的输入本身就不是位级别相同的，那么我们自然无法期望得到位级别相同的输出！

这道理看似简单，却揭示了问题的核心。对于大多数机器学习模型而言，只要输入保持位级别一致，模型就能产生位级别一致的结果。这在 PyTorch 的 torch.nn.Linear、torch.nn.Conv2d、torch.nn.BatchNorm2d 等常见模块中都是成立的。少数例外，如依赖内部状态（例如训练模式下的 dropout 或 batch norm）或非确定性算法选择（如 cuDNN 的卷积算法），但这些在 LLM 推理中并非主要问题。在 LLM 推理的语境下，我们关注的底层内核确实是确定性的。

那么，如果内核本身是确定性的，那些导致差异的“非相同输入”又是从何而来的呢？答案直指：动态内核调度（Dynamic Kernel Dispatch）。

4. 动态内核调度：性能优化背后的“随机性”隐患

GPU 之所以能提供强大的计算能力，正是因为它们是高度通用的计算设备。然而，这种通用性也伴随着一个挑战：如果不针对特定的输入规模、数据类型和硬件平台精心调优所使用的算法，GPU 的性能往往会大打折扣。因此，GPU 通常会拥有同一内核的多个“版本”，每个版本都针对不同的场景进行了专门优化。

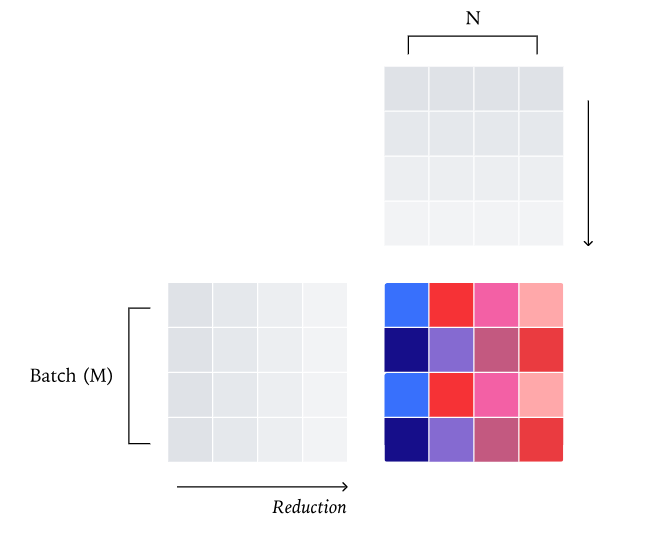
举例来说，一个处理 2048x2048 矩阵的 bfloat16 矩阵乘法内核，其实现方式可能与处理 4096x4096 矩阵的内核大相径庭。这是因为矩阵乘法的最优算法会随着矩阵大小的变化而调整。所以，GPU 会根据矩阵的具体尺寸来选择不同的内核版本。

而内核的差异不仅体现在输入尺寸上，还与硬件平台息息相关。比如，为 NVIDIA A100 GPU 优化的 CUDA 内核，很可能与为 NVIDIA H100 GPU 优化的内核有所不同，因为底层硬件架构的差异会影响最优算法的选择。

这种根据输入大小、输入类型和硬件动态选择最佳内核的过程，就是所谓的“内核调度（Kernel Dispatch）”。更重要的是，这是一个动态过程，意味着最终调度哪个内核，完全取决于实际传递给 GPU 的输入数据。

4.1 动态内核调度如何“悄无声息”地引入非确定性？

问题的关键在于：对于许多计算操作（尤其是归约操作），不同的内核版本虽然在数学上实现了完全相同的功能，但它们在底层执行时，可能会以不同的顺序累加浮点数。正如我们之前讨论的，这种累加顺序的微小变化，足以导致最终结果的差异。

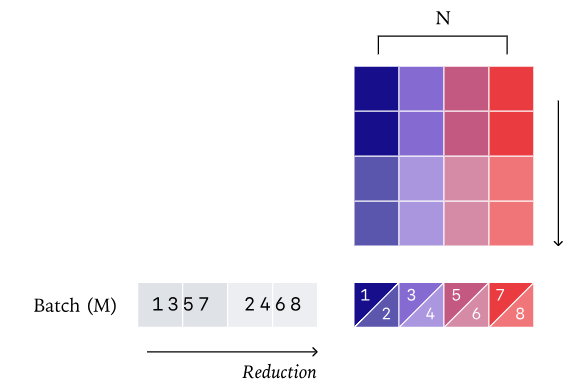
因此，如果你的内核调度机制是动态的，那么即使每个被调度的独立内核本身都是确定性的，你依然可能得到非确定性的推理结果！

让我们通过一个简单的例子来理解。假设你需要计算 sum(A) + sum(B)。完成这个任务有很多种方法：你可以先分别计算 sum(A) 和 sum(B)，然后将两个结果相加；或者，你可以将 A 和 B 合并成一个大数组 C，再计算 sum(C)。从数学角度看，这两种方法的结果应该一致。但如果涉及浮点数运算，由于其非结合性，这两种方法可能会产生细微的数值差异。

现在想象一下，如果内核调度是动态的，那么根据 A 和 B 的具体数值（例如它们的长度或内部分布），GPU 可能会在不同时间点选择不同的内核来计算 sum(A)、sum(B) 甚至 sum(C)。一旦选择的内核不同，其浮点数累加顺序就可能改变，进而导致最终结果的差异。这便是 LLM 推理中非确定性产生的一个重要原因。

在 LLM 推理中，最容易受到这种动态调度影响并导致非确定性的操作，主要集中在 RMSNorm 和注意力（Attention）机制。

4.2 RMSNorm：归一化层的“微妙”挑战

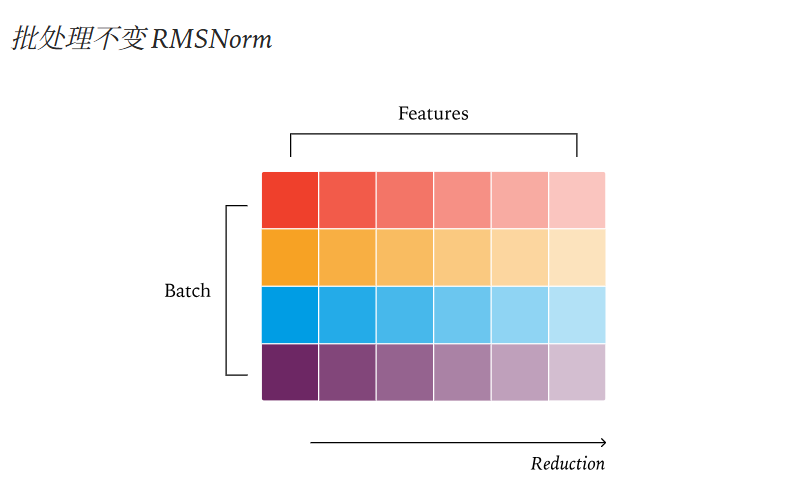
RMSNorm 是 LLM 中一个非常常见的归一化层，它通过计算输入数据的均方根来对其进行缩放。这个均方根的计算过程本质上是一个归约操作（即对平方项求和），而这个归约操作可以通过多种不同的方式实现。

举个例子，如果你的批次（batch）中包含多个序列，并且这些序列的长度各不相同，那么 RMSNorm 内核可能会针对每个序列选择不同的归约策略。这种动态选择机制，恰恰是导致非确定性结果的潜在原因。

要解决这个问题，关键在于采用批次不变（batch-invariant）的 RMSNorm 内核。一个批次不变内核的特点是，无论输入批次的大小或序列长度如何变化，它始终采用相同的、固定的归约策略。这样一来，就能确保 RMSNorm 的计算结果始终是确定性的，从而消除了这一环节的随机性。

4.3 注意力机制（Attention）：高性能下的“确定性”困境

注意力机制是 LLM 的另一个核心组件，它通过计算查询（queries）和键（keys）之间的相似度来生成权重，进而对值（values）进行加权求和。这个加权求和同样是一个归约操作，其实现方式也多种多样。

特别是，注意力机制常常会用到分段归约内核（split-reduction kernel），例如我们熟悉的 FlashAttention 或 FlashDecoding。这是因为，如果不沿着归约维度进行并行化，我们只能沿着批次维度、头维度和“查询长度”维度进行并行。而在注意力的解码阶段，查询长度通常非常小，这意味着除非批次大小非常大，否则 GPU 的算力往往无法得到充分利用。为了提高效率，分段归约内核应运而生。

然而，问题在于，不同的分段归约策略可能会导致非确定性结果。例如，当处理一个非常长的 KV 缓存时，即使只处理一个请求，注意力内核也可能需要很长时间，而且其内部的累加顺序也可能因调度策略而异。

传统的固定分段 KV 策略（如 FlashDecode）：当查询长度变得很小（例如在解码过程中），内核的并行度会急剧下降。此时，为了维持 GPU 饱和度，我们通常需要沿着归约维度（即 KV 维度）再次进行分段。典型的做法是根据所需的并行度，将 KV 维度均匀划分。例如，如果 KV 长度为 1000，需要 4 个分段，每个核心将处理 250 个元素。

不幸的是，这种策略会破坏批次不变性。因为精确的归约策略会依赖于当前请求中处理的查询 token 数量，从而在不同请求或不同批次之间引入非确定性。

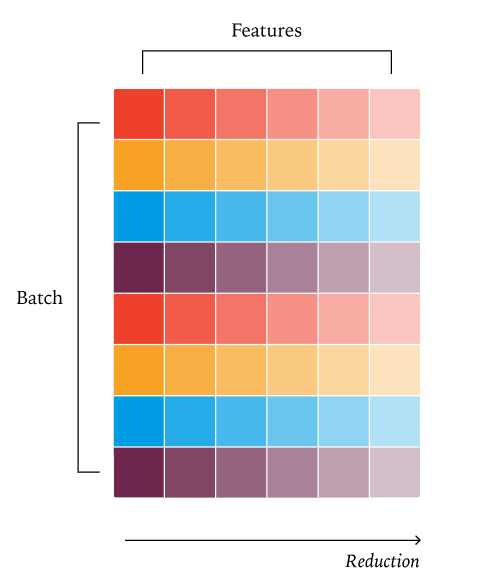
此外，注意力中常用的分段归约策略也对批次不变性构成了挑战。例如，FlashInfer 的“平衡调度算法”会选择能够使所有 GPU 核心饱和的最大分段大小，这使得归约策略不再是“批次不变”的。与 RMSNorm/Matmuls 不同，仅仅固定分段数量，而不考虑批次大小，是不足以保证确定性的。

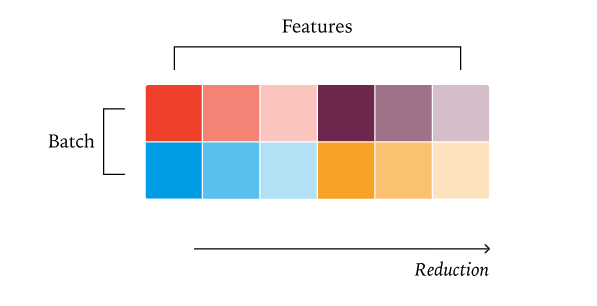
批次不变的固定大小分段 KV 策略：为了真正实现批次不变性，我们必须采纳一种“固定分段大小”的策略。这意味着我们不再固定分段的数量，而是固定每个分段处理的数据大小，然后根据总长度得到相应数量的分段。例如，如果 KV 长度为 1000，我们可以将其分成三个长度为 256 的固定大小分段，以及一个长度为 232 的分段。通过这种方式，我们可以确保无论处理多少 token，累加的归约顺序始终保持一致，从而彻底消除动态调度带来的非确定性！

这种方法虽然需要对 FlexAttention 进行一些内部调整（这些更改尚未在我们的代码发布中），但我们预计将在不久的将来将其贡献到上游社区，以期推动 LLM 推理的确定性发展。

5. 实现确定性推理：工具与实践

为了演示如何在 LLM 推理中实现确定性，我们提供了一个基于 vLLM 的解决方案，它巧妙地利用了 vLLM 的 FlexAttention 后端和 PyTorch 的 torch.Library 机制。通过 torch.Library，我们能够以一种非侵入式的方式，替换掉 PyTorch 中大多数相关的运算符，使其采用批次不变的实现。

如果你对此感兴趣，可以在 thinking-machines-lab/batch-invariant-ops 找到这个“批次不变”内核库，同时也有在“确定性”模式下运行 vLLM 的示例，方便你进行实践和验证。

6. 实验验证：非确定性的影响与确定性方案的成效

6.1 LLM 推理的非确定性程度究竟有多高？

为了量化 LLM 推理的非确定性程度，我们进行了一项实验：使用 Qwen/Qwen3-235B-A22B-Instruct-2507 模型，在温度设置为 0 的条件下，对相同的提示词“告诉我关于理查德·费曼”（非思维模式）进行 1000 次补全采样，每次生成 1000 个 token。令人惊讶的是，即便在理论上应该确定性的设置下，我们仍然得到了 80 个独特的补全结果，其中最常见的补全出现了 78 次。

深入分析这些差异，我们发现补全结果在前 102 个 token 中是完全相同的！分歧首次出现在第 103 个 token。所有补全都始于“Feynman was born on May 11, 1918, in”，但其中 992 个补全继续生成“Queens, New York”，而另外 8 个补全则生成了“New York City”。这种细微但关键的差异，足以影响下游应用。

然而，当我们启用我们开发的批次不变内核后，所有 1000 个补全结果都变得完全一致。这正是我们在数学上对采样器所期望的确定性行为，也验证了批次不变内核在消除非确定性方面的有效性。

6.2 性能考量：确定性是否意味着牺牲效率？

目前，我们尚未将大量精力投入到批次不变内核的性能优化上。但为了确保其在实际应用中的可用性，我们进行了一些初步的性能测试。

我们搭建了一个 API 服务器，使用单块 GPU 运行 Qwen-3-8B 模型，并请求 1000 个序列，每个序列的输出长度在 90 到 110 个 token 之间。

从结果可以看出，性能上的主要下降，源于 vLLM 中 FlexAttention 集成尚未进行大量优化。尽管如此，我们的确定性方案在性能上并不是“灾难性的”，依然具备可用的效率。

在部署大语言模型时，除了推理性能，成本也是一个关键考量。特别是对于需要大量算力的 LLM 推理任务，传统的云服务器部署成本可能居高不下。我们发现，利用像共绩算力这样的按秒计费 Serverless GPU 服务，可以显著降低 LLM 的部署和运行成本。例如，按秒计费的 4090 显卡，跑一次推理可能只需几毛钱，这极大减轻了测试和迭代的财务负担，让开发者能更灵活地进行实验和生产部署。这种经济高效的方案，为追求可复现性和性能平衡的 LLM 部署提供了新的选择。

6.3 真正的在线强化学习（True On-policy RL）：确定性带来的新可能

研究人员已经指出，训练和推理之间存在的数值差异，会隐式地将我们的在线强化学习（On-policy RL）转化为离线强化学习（Off-policy RL）。这意味着训练时模型学到的策略，在实际推理时可能无法完全复现，从而影响学习效率和效果。

显然，如果连两个相同的推理请求都无法获得位级别相同的结果，那么在训练和推理之间实现位级别完全一致更是无从谈起。然而，确定性推理的实现，为我们提供了一个修改训练堆栈的契机，使得在采样（sampling）和训练之间也能获得位级别相同的结果。这将最终带来真正的在线强化学习。

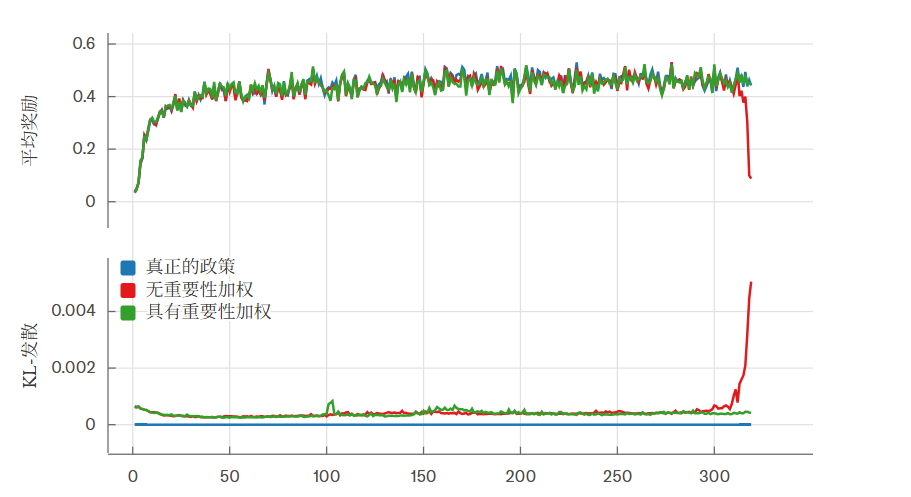
我们在 Bigmath 上的 RLVR 环境中进行了实验，RL 策略由 Qwen 2.5-VL instruct 8B 初始化，最大 rollout 长度为 4096。实验结果令人鼓舞：

• 如果在没有离线校正（即重要性采样）的情况下进行训练，我们的奖励会在训练过程中途崩溃。
• 而通过添加离线校正项，训练可以顺利进行。
• 最重要的是，当我们实现了采样器和训练器之间的位级别相同结果时，我们就达到了完全在线（即 KL 散度为 0）的状态，训练也能够平稳顺利地进行。

我们还绘制了采样器和训练器之间 logprobs 的 KL 散度图，可以看到三种运行方式有着显著不同的行为。在使用重要性采样时，KL 散度保持在 0.001 左右，偶尔出现峰值。然而，在没有重要性采样的情况下运行时，KL 散度最终会在奖励崩溃的同时出现峰值。而当我们运行“真正的在线强化学习”时，KL 散度则稳定地保持在 0，这清晰地表明了训练策略和采样策略之间没有任何分歧。蓝线显示的“真正的在线强化学习”并非 bug，它仅仅是一条平坦的 0 线，完美诠释了确定性带来的精确控制。

7. 总结与展望：告别“玄学”，拥抱可控 AI

现代软件系统往往构建在层层抽象之上。在机器学习领域，当我们遭遇非确定性和细微的数值差异时，往往会有一种“大事化小”的倾向。毕竟，我们的系统本来就“概率性”的，再多一点非确定性又何妨？单元测试失败时，调高一下 atol/rtol 不就行了？训练器和采样器之间 logprobs 的差异，可能也不是什么真正的 bug，对吧？

但我们坚定地拒绝这种“失败主义”的态度。只要我们愿意付出努力，我们就能够理解这些非确定性的根本原因，并找到切实可行的解决方案！我们希望这篇博文不仅能为社区提供关于如何在推理系统中解决非确定性的深刻理解，更能激励更多同行深入探索自己的系统，最终实现对 AI 系统的全面掌控。